| Citation: |
Hongyao Xie. The role of off-centering behavior and acoustic-optical phonon coupling in heat transport[J]. Materials Lab, 2023, 2(1): 220051. doi: 10.54227/mlab.20220051
|
The role of off-centering behavior and acoustic-optical phonon coupling in heat transport
Published as part of the Virtual Special Issue "Mercouri G. Kanatzidis at 65"
-
Abstract
Understanding the nature of phonon transport in solids and exploring the way to minimize the thermal conductivity are important in many fields, including the development of efficient thermoelectric materials. For a long time, the contribution of optical phonons to the lattice thermal conductivity is considered to be very small and negligible. Until recent decade, a series of studies have shown that, for some materials with special electronic configuration, optical phonons can dramatically affect the lattice thermal conductivity. Specifically, in these materials, part of their cations would be off-centering from their equilibrium positions and lead to the local distortion of the coordination structure. This off-centering behavior would introduce some low-frequency optical phonons, which can couple with the acoustic phonons and cause additional phonon scattering, thus, it is very effective to suppress the lattice thermal conductivity. This perspective clarifies the lattice dynamics of off-centering behavior and illustrates how this off-centering behavior could lead to the acoustic-optical phonon coupling. This paper also demonstrates the off-centering behavior can be introduced into a material by using the lone pair element doping and the weak sd3 orbital hybridization, and proposes a strategy to design materials with low thermal conductivity based on this.
-
-
Author Biography
Hongyao Xie is now a postdoctoral research fellow at Northwestern University, Evanston. He received his Ph.D. degree from Wuhan University of Technology, China, in 2018. His research focuses on the electron and phonon transport behaviors in semiconductor. -
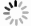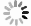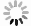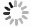
References
1. Q. Yan, M. G. Kanatzidis, Nat. Mater., 2022, 21, 503 2. Q. Bingchao, Z. Li-Dong, Materials Lab, 2022, 1, 220004 3. F. Yuting, T. Gangjian, Materials Lab, 2022, 1, 220008 4. J. He, T. M. Tritt, Science, 2017, 357, eaak9997 5. W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis, G. J. Snyder, Angew. Chem. Int. Ed., 2016, 55, 6826 6. L. Dongrui, Q. Bingchao, Z. Li-Dong, Materials Lab, 2022, 1, 220006 7. R. Hanus, M. T. Agne, A. J. E. Rettie, Z. Chen, G. Tan, D. Y. Chung, M. G. Kanatzidis, Y. Pei, P. W. Voorhees, G. J. Snyder, Adv. Mater., 2019, 31, e1900108 8. Z. Chen, X. Zhang, Y. Pei, Adv. Mater., 2018, 30, e1705617 9. J. Callaway, H. C. von Baeyer, Phys. Rev., 1960, 120, 1149 10. B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto, D. Vashaee, X. Chen, J. Liu, M. S. Dresselhaus, G. Chen, Z. Ren, Science, 2008, 320, 634 11. Z. Fudong, W. Di, H. Jiaqing, Materials Lab, 2022, 1, 220012 12. B. Yu, M. Zebarjadi, H. Wang, K. Lukas, H. Wang, D. Wang, C. Opeil, M. Dresselhaus, G. Chen, Z. Ren, Nano Lett., 2012, 12, 2077 13. H. Xie, X. Su, X. Zhang, S. Hao, T. P. Bailey, C. C. Stoumpos, A. P. Douvalis, X. Hu, C. Wolverton, V. P. Dravid, C. Uher, X. Tang, M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 10905 14. G. Tan, S. Hao, R. C. Hanus, X. Zhang, S. Anand, T. P. Bailey, A. J. E. Rettie, X. Su, C. Uher, V. P. Dravid, G. J. Snyder, C. Wolverton, M. G. Kanatzidis, ACS Energy Lett., 2018, 3, 705 15. Y. Xiao, Y. Wu, P. Nan, H. Dong, Z. Chen, Z. Chen, H. Gu, B. Ge, W. Li, Y. Pei, Chem., 2020, 6, 523 16. M. Hong, T. C. Chasapis, Z. G. Chen, L. Yang, M. G. Kanatzidis, G. J. Snyder, J. Zou, ACS nano, 2016, 10, 4719 17. C. Fu, S. Bai, Y. Liu, Y. Tang, L. Chen, X. Zhao, T. Zhu, Nat. Commun., 2015, 6, 8144 18. H. Xie, S. Hao, S. Cai, T. P. Bailey, C. Uher, C. Wolverton, V. P. Dravid, M. G. Kanatzidis, Energy Environ. Sci., 2020, 13, 3693 19. T. M. Tritt, Thermal conductivity: theory, properties, and applications, Springer Science & Business Media, Germany, 2005. 20. Z. Li, H. Xie, S. Hao, Y. Xia, X. Su, M. G. Kanatzidis, C. Wolverton, X. Tang, Phys. Rev. B, 2021, 104, 245209 21. E. S. Božin, C. D. Malliakas, P. Souvatzis, T. Proffen, N. A. Spaldin, M. G. Kanatzidis, S. J. L. Billinge, Science, 2010, 330, 1660 22. Y. Zhang, X. Ke, P. R. Kent, J. Yang, C. Chen, Phys. Rev. Lett., 2011, 107, 175503 23. O. Delaire, J. Ma, K. Marty, A. F. May, M. A. McGuire, M. H. Du, D. J. Singh, A. Podlesnyak, G. Ehlers, M. D. Lumsden, B. C. Sales, Nat. Mater., 2011, 10, 614 24. Z.-Z. Luo, S. Hao, X. Zhang, X. Hua, S. Cai, G. Tan, T. P. Bailey, R. Ma, C. Uher, C. Wolverton, V. P. Dravid, Q. Yan, M. G. Kanatzidis, Energy Environ. Sci., 2018, 11, 3220 25. S. Cai, S. Hao, Z.-Z. Luo, X. Li, I. Hadar, T. P. Bailey, X. Hu, C. Uher, Y.-Y. Hu, C. Wolverton, V. P. Dravid, M. G. Kanatzidis, Energy Environ. Sci., 2020, 13, 200 26. K. R. Knox, E. S. Bozin, C. D. Malliakas, M. G. Kanatzidis, S. J. L. Billinge, Phys. Rev. B, 2014, 89, 014102 27. M. Dutta, M. V. D. Prasad, J. Pandey, A. Soni, U. V. Waghmare, K. Biswas, Angew. Chem. Int. Ed., 2022, 134, e202200071 28. H. Xie, S. Hao, J. Bao, T. J. Slade, G. J. Snyder, C. Wolverton, M. G. Kanatzidis, J. Am. Chem. Soc., 2020, 142, 9553 29. H. Xie, E. S. Bozin, Z. Li, M. Abeykoon, S. Banerjee, J. P. Male, G. J. Snyder, C. Wolverton, S. J. L. Billinge, M. G. Kanatzidis, Adv. Mater., 2022, 34, e2202255 30. H. Xie, S. Hao, T. P. Bailey, S. Cai, Y. Zhang, T. J. Slade, G. J. Snyder, V. P. Dravid, C. Uher, C. Wolverton, M. G. Kanatzidis, J. Am. Chem. Soc., 2021, 143, 5978 31. H. Xie, Y. Liu, Y. Zhang, S. Hao, Z. Li, M. Cheng, S. Cai, G. J. Snyder, C. Wolverton, C. Uher, V. P. Dravid, M. G. Kanatzidis, J. Am. Chem. Soc., 2022, 144, 9113 32. H. Xie, X. Su, S. Hao, C. Zhang, Z. Zhang, W. Liu, Y. Yan, C. Wolverton, X. Tang, M. G. Kanatzidis, J. Am. Chem. Soc., 2019, 141, 18900 -
Rights and permissions
This is an open access article under the terms of the Creative Commons Attribution License, which permits use, distribution and reproduction in any medium, provided the original work is properly cited.
Figures(3)
Information
Article Metrics
Export File
Citation
Hongyao Xie. The role of off-centering behavior and acoustic-optical phonon coupling in heat transport[J]. Materials Lab, 2023, 2(1): 220051. doi: 10.54227/mlab.20220051
Format
Content
DownLoad:
-
Figure 1.
The schematic diagram shows the phonon dispersion for the usual case and the acoustic-optical (A-O) phonon coupling case. Usually, the optical modes have much higher frequency than that of the acoustic modes, and the interaction between these phonons is weak. In the A-O phonon coupling case, part of the optical phonons has the extremely low frequency, which sit very close to the acoustic mode and cause the strong interaction between these phonons. The avoided crossing phenomenon is the characteristic feature of the A-O phonon coupling.
-
Figure 2.
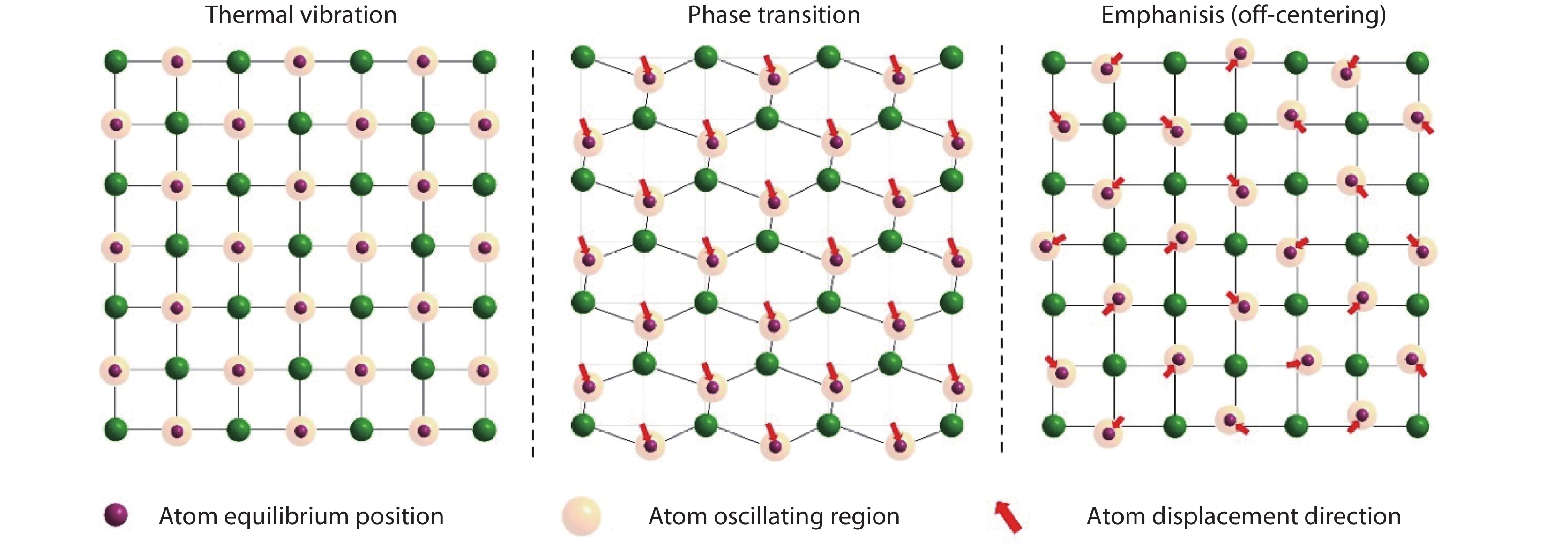
The schematic diagram illuminates the concepts of thermal vibration, phase transition and off-centering behavior. The thermal vibration is a general effect and indicates all atoms in the crystal are dynamic variation caused by thermal energy. The phase transition indicates the atoms in the lattice move from their high energy positions to another low energy positions, their new equilibrium positions are equivalent in crystallography, and this driven by the energy and results in the global crystal symmetry breaking. However, for the off-centering behavior, the moving atoms are dynamically off-centered, and move incoherently in different directions. In this case, the local symmetry is broken, but the crystal structure still retains the original crystallographic symmetry on average.
